Based on the graph, we can see the function has two asymptotes at x=-2 and x=2.
Therefore, the denominator of the function must equal 0 at those values.
We can discard options A and D since the denominator only equals 0 for a single value: 2.
In order to determine wether option B or C fits the graph better, we'll need to see what happens when we take values close to the discontinuities.
Let's consider the function
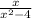
We know at x=-2 it has an asymptote because the denominator equals 0 at that point. Let's take a value close to -2 but less than it, for example, -3
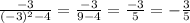
However, in the given graph we can see that for x values below -2, the function is positive. Thus we can discard option B.
By process of elimination, we could choose option C, but let's make sure it's actually correct.
Similarly as we did before, let's take values close to the discontinuities and observe how the function behaves.
Let's take x=-3, x=-1, x=1 and x=3
The function in question is
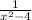
for x=-3:
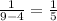
Since the function is positive, it behaves similarly to the one we were given.
For x=-1:
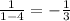
which behaves as the given function.
For x=1 we'll get the same result as x=-1 since the x is squared, thus the function will be negative which is the same as the given function.
For x=3 we'll get the same result as x=-3 by a similar argument as before. Thus the function will be positive and behave in line with the given graph.
With all these arguments, we can finally say that option C is the best fit for the given graph.