EXPLANATION
Let's see the facts:
Heights of 8th grade boys ---------------> Normally distributed
Mean= 50 inches
Standard deviation= 4 inches
d) Probability that boy shorter than 56 inches:
x=56
P(x<56)
We know that z-score=
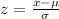
Replacing terms:

P-value from Z-table =
P(x<56) = 0.93319
Answer: The probability that an 8th grade boy will be shorter than 56 inches is 0.93319*100= 93.3%.
c) Percentage of 8th grade boys that are between 56 and and 60 inches tall is:
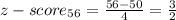
P-value from Z-table =
P(x<60) = 0.93319
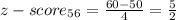
P-value from Z-table =
P(x<60) = 0.99379
Then, subtracting both probabilities.
P(56
Answer: the percentage of 8th grade boys that are between 56 and 60 inches tall is 0.0606*100 = 6.06%.
a) We have that,
According to the Empirical Rule, we can assevere that 50+- 3σ = 50+- 3*4 ---->
50 + 12 = 62 inches
50 - 12 = 38 inches
About 99.7% of 8th grade boys height will fall between 38 inches and 62 inches.
Answer: Approximately 99.7% of the heights fall between 38 inches and 62 inches.
b) According to the Empirical Rule, we can assevere that around 68% of the data will fall within one standard deviation of the mean. As we already know, the standard deviation σ is a natural yardstick for any measurements that follow a normal distribution.
So, 50 +- σ = 50 +- 4 ---->
50 + σ = 50 + 4 = 54
50 - σ = 50 - 4 = 46
Answer: About 68% of 8th grade boys height will fall between 46 inches and 54 inches.