Question

What is the carrying capacity of an environment for a population with rmax = 3, that exhibits no population growth when N = 3000?

Answer 1

Let's define what our logistical growth formula is:

`(dN)/(dt)=r_(max)N\bigg((K-N)/(N)\bigg)`
`(dN)/(dt)=r_(max)N\bigg((K-N)/(N)\bigg)`

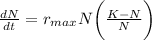
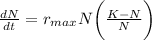
Where r (max) is the max per capita growth rate of population, N is the population size, and K is the carrying capacity.

If we are given that r (max) is equal to 3 and that the given population exhibits no growth when N = 3000, we can find what the carrying capacity is by substituting into our formula:

`(dN)/(dt)=3(3000)\bigg((K-3000)/(K)\bigg)`

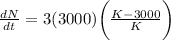
Let's simplify this a little more:

`(dN)/(dt)=9000\bigg((K-3000)/(K)\bigg)`

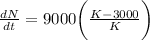
If we are trying to find the carrying capacity, then recall that the amount of change in the population with respect to time (dN/dt) must equal 0. Therefore, we can set our derivative to be equal to 0 and find the value of K:

`0=9000\bigg((K-3000)/(K)\bigg)`

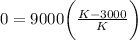
Interpreting this, it means that whatever the growth is 0, it is dependent on the value K carrying capacity. When we solve this out, we can obtain an answer for the carrying capacity:

`K=3000`

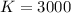
∴ the carrying capacity K of this environment is equal to 3000 organisms.