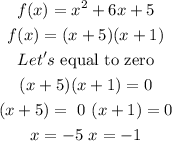Solution: X-value of vertex=-3
Y-value of vertex=-4
Zeros of the parabola: X=-5 and x=-1
Analysis
We can find the x-coordinate of the vertex, calculating -b/2a. First, we identify the a and b values of y=ax^2+bx+c of your quadratic equation.
b=6
a=1
![\begin{gathered} -(b)/(2a)=-(6)/(2(1))=-3 \\ \\ After\text{ we find x-coordinate, we can find y-coordinate of the vertex replacing x-value.} \\ f(x)=x^2+6x+5\text{ = }^^(-3\text{ }^2)+6(-3)+5 \\ f(x)\text{ = 9}-18+5 \\ f(x)=-4 \end{gathered}]()
Now, let's find the zeros of the parabola. We factorize the quadratic equation: