Given the following variation
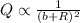
Introducing the constant of proportionality c as shown below
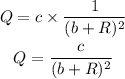
Q=4, when b=2, R= 8
Let use the above values of Q, b, and R to find the value of c as shown below:
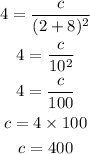
Let us substitute c in the formula as shown below

Hence, the specific formula to describe the variation is
Q= 400/(b+R)²