Answer
The exact value of the lateral surface area = 395 cm²
The exact value of the total surface area = 572 cm²
Step-by-step explanation
The solid shape is a cone with a height of 15 cm and the diameter of the base of the solid shape is 15 cm.
The Lateral Surface Area of the Solid Shape:
The formula to calculate the lateral surface area (LSA) of a cone is given by:
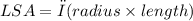
The radius will be = diameter/2 = 15cm/2 = 7.5 cm
To find legth, we use Pythagoras rule:
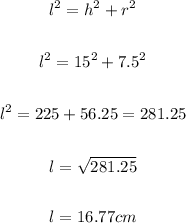
Put π = 3.14, r = 7.5 cm, and l = 16.77 cm into the lateral surface area formula:
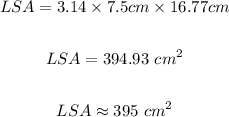
Therefore, The exact value of the lateral surface area = 395 cm²
Total Surface Area of the Solid Shape:
To find the exact value for the total surface area of the solid shape, we use the total surface area (TSA) formula of a cone which is:
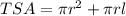
put π = 3.14, r = 7.5 cm, and l = 16.77 cm

The exact value of the total surface area = 572 cm²