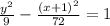Question

Writing an equation of a hyperbola give me the Foci and vertices

Answer 1

Given the Foci of the hyperbola:

`\begin{gathered} (-1,-9) \\ (-1,9) \end{gathered}`

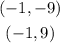
And the Vertices:

`\begin{gathered} (-1,-3) \\ (-1,3) \end{gathered}`

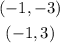
You can plot the Foci on a Coordinate Plane:

Notice that the blue line represents the Vertical Transverse Axis. Then, the equation has this form:

`((y-k)^2)/(a^2)-((x-h)^2)/(b^2)=1`

You need to find the Center using the Midpoint Formula, in order to find the Midpoint between the Foci and the Midpoint between the vertices:

`M=((x_1+x_2)/(2),(y_1+y_2)/(2))`

- For the Foci:

`M=((-1-1)/(2),(-9+9)/(2))=(-1,0)`

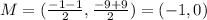
- For the Vertices:

`M=((-1-1)/(2),(-3+3)/(2))=(-1,0)`

Therefore:

`\begin{gathered} h=-1 \\ k=0 \end{gathered}`

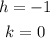
Now you need to find "a". This is the distance from the center to the vertices:

`a=3-0=3`

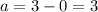
Find "b" with this formula:

`b^2=c^2-a^2`

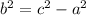
Knowing that "c" is the distance from the Foci to the center:

`c=9`

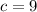
You get:

`b^2=9^2-3^2=72`

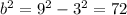
Therefore, you can write this equation:

`(y^2)/(9)-((x+1)^2)/(72)=1`

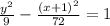
Hence, the answer is:

`(y^2)/(9)-((x+1)^2)/(72)=1`