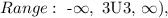ANSWER
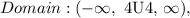
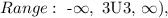
Step-by-step explanation
Given:
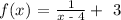
Desired Outcome:
1. Domain
2. Range
Determine the domain of the function
Note: We want to include only input values that do not require the denominator to be 0 when there is a denominator. As a result, we'll set the numerator to 0 and solve for x.
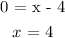
We'll now remove 4 from the domain. All of the answers are real numbers x > 4 or x < 4. We will also use Union notation to combine the two sets.
That is:
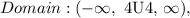
Determine the range of the function
Set x to 4 to find y
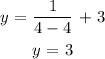
We'll also remove 3 from the range. All of the answers are real numbers y > 3 or y < 3. We will also use Union notation to combine the two sets.
That is: