Question

Find the interval on which the curve of y equals the integral from 0 to x of 2/(1+3t+t^2), dt is concave up.

How do I do this problem? I took notes on the lesson my course is telling me its from, but I have no idea how to go about it.

Answer 1

By the fundamental theorem of calculus, the first derivative of


`y=\displaystyle\int_0^x\frac2{1+3t+t^2}\,\mathrm dt`

is


`y'=\displaystyle(\mathrm d)/(\mathrm dx)\int_0^x\frac2{1+3t+t^2}\,\mathrm dt=\frac2{1+3x+x^2}`

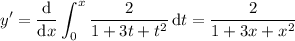
Then the second derivative is


`y''=((1+3x+x^2)(0)-2(3+2x))/((1+3x+x^2)^2)=-(2(2x+3))/((1+3x+x^2)^2)`

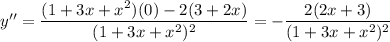
From here you can proceed with determining the concavity of
`y` by finding the possible inflection points (when
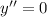
`y''=0` or undefined). Since the denominator is positive for all
`x`, you know that
`y''` is defined for all
`x`. So you're left with solving


`y''=-(2(2x+3))/((1+3x+x^2)^2)=0`

`\implies 2x+3=0`

`\implies x=-\frac32`

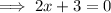
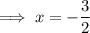
So you have two intervals to consider,
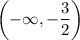
`\left(-\infty,-\frac32\right)` and
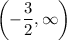
`\left(-\frac32,\infty\right)`. Check the sign of
`y''` in both of these intervals; if
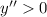
`y''>0` on some interval, then
`y` is concave upward on that interval.