Question

Determine the axis of symmetry and the vertex of the given function.

y = 2x2 − 12x + 21

Axis of symmetry

Answer 1

The vertex is (3,3) and the axis is 3

Answer 2

Vertex is (3,3)

Axis of symmetry is x=3

Explanation:

Given : Function
`y = 2x^2 -12x + 21`

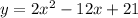
To find : The axis of symmetry and the vertex of the given function.

Solution :

The given function is in the form of quadratic equation
`y=ax^2+bx+c`

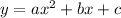
Comparing with the given function
`y = 2x^2 -12x + 21`

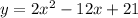
a=2 , b=-12 and c=21

x-coordinate of axis of symmetry and vertex

Axis of symmetry is given by
`x=-(b)/(2a)`

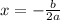
Substitute the value,

`x=-(-12)/(2(2))`

`x=(12)/(4)`

`x=3`

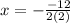
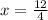
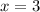
For y-coordinate of axis substitute x=3 in y

`y = 2(3)^2 -12(3) + 21`

`y = 2(9)-36+ 21`

`y = 18-15`

`y = 3`

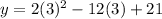
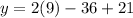
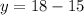
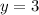
Therefore, The vertex of function is (3,3).