Question

Consider the electric force between a pair of charged particles a certain distance apart. By Coulomb's Law, if the charge on one of the particles is doubles, the force is

Answer 1

Doubled as well. Using what I call "Method of Simplest Integers," insert all charges and distance as just 1 (ignore k, because it is a constant), so

Fe=k(1*1)/(1^2)=k(1)/1=k(1)

Since one of the charges is doubled,

Fe'=k(2*1)/(1^2)'k(2)/1=k(2)

Set Fe and Fe' side by side and compare their outcomes. cancel out k, because it's constant, and find out what multiple makes Fe becomes Fe'. In this case, it is 2. So the force would be doubled if one of the charges is doubled.

Answer 2

The Force is Doubled

Step-by-step explanation:

From Coulomb's Law the force is given as

`Force=k(q_(1)q_(2) )/(r^(2) )`

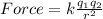
As we have given that charge are doubled on one plate then the force will be:

`Force=k(q_(1)q_(2) )/(r^(2) )\\if\\ q_(1)=2q_(1)\\then\\Force=k(2q_(1)q_(2) )/(r^(2) )\\So\\Force=2(k(q_(1)q_(2) )/(r^(2) ))\\Force=2*(Force)`

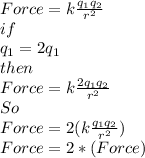
So the Force is Doubled

If the charges are doubled on both plate then the force will be:

`Force=k(q_(1)q_(2) )/(r^(2) )\\as\\ q_(1)=2q_(1)\\and\\q_(2)=2q_(2)\\then\\Force=k(2q_(1)2q_(2) )/(r^(2) )\\So\\Force=4(k(q_(1)q_(2) )/(r^(2) ))\\Force=4*(Force)`

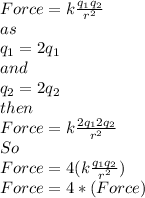
So the Force is Quadrupled