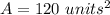You can identify that the figure has four sides and all the sides have equal length.
By definition, a rhombus is a quadrilateral whose sides have equal length, its opposite sides are parallel and its diagonals bisect each other at Right angles (a Righ angle is an angle that measures 90 degrees).
You can identify this triangle inside the rhombus:
Knowing that the diagonals bisect each other, you can determine that:
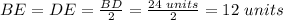
Then, you can use the following Inverse Trigonometric Function to find the measure of the angle BCE:
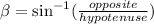
In this case:
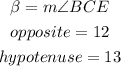
Substituting values and evaluating, you get:
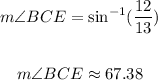
Now you can determine that:
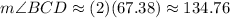
Knowing this angle, you can use this formula to find the area of the rhombus:
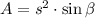
In this case:
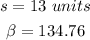
Therefore, substituting values and evaluating, you get:
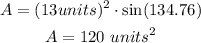
The answer is: