Question

A regular heptagon has a radius of approximately 27.87 cm and the length of each side is 24.18 cm. What is the approximate area of the heptagon rounded to the nearest whole number? Recall that a heptagon is a polygon with 7 sides.

Answer 1

If you know the side length, you don't need the radius to calculate the area. The area for any regular polygon is:

A(n,s)=(ns^2)/(4tan(180/n)), where n=number of sides and s=length of sides.

The above is derived by dividing the polygon into n triangles...anyway, in this case:

A=(7*24.18^2)/(4tan(180/7)

A=1023.1767/tan(180/7)

A=2124.65 cm^2 (to nearest one-hundredth)

Answer 2

`2124.65\text{ cm}^2`.

Explanation:

We have been given that a regular heptagon has a radius of approximately 27.87 cm and the length of each side is 24.18 cm.

We will use area of a heptagon formula to find the area of our given heptagon.

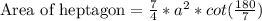`\text{Area of heptagon}=(7)/(4)*a^2*cot((180)/(7))`, where, a represents each side of heptagon.

Upon substituting a=24.18 cm we will get,

`\text{Area of heptagon}=(7)/(4)*\text{(24.18 cm)}^2*cot((180)/(7))`

`\text{Area of heptagon}=(7)/(4)*584.6724\text{ cm}^2*2.0765213965692558`

`\text{Area of heptagon}=7*146.1681\text{ cm}^2*2.0765213965692558`

`\text{Area of heptagon}=2124.648310021\text{ cm}^2\approx 2124.65\text{ cm}^2`

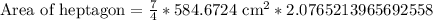
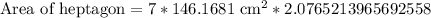
Therefore, area of our given heptagon will be approximately
`2124.65\text{ cm}^2`.