Question

The volumes of two similar solids are 210 m3 and 1,680 m3. The surface area of the larger solid is 856 m2.

What is the surface area of the smaller solid?

Answer 1

`\bf \qquad \qquad \textit{ratio relations} \\\\ \begin{array}{cccllll} &Sides&Area&Volume\\ &-----&-----&-----\\ \cfrac{\textit{similar shape}}{\textit{similar shape}}&\cfrac{s}{s}&\cfrac{s^2}{s^2}&\cfrac{s^3}{s^3} \end{array}\\\\\\\\ -----------------------------\\\\ \cfrac{\sqrt[3]{s^3}}{\sqrt[3]{s^3}}=\cfrac{√(s^2)}{√(s^2)}=\cfrac{s}{s}\implies \cfrac{\sqrt[3]{210}}{\sqrt[3]{1680}}=\cfrac{√(A)}{√(856)}`

solve for A

Answer 2

The surface area of smaller solid is:

214 m²

Explanation:

Let A,V be the surface area and the volume of larger solid.

and A',V' be the surface area and volume of other solid.

We know that the ratio of volume to the surface area of the solid is given by:

`(√(A))/(√(A'))=\frac{\sqrt[3]{V}}{\sqrt[3]{V'}}`

On taking power 6 on both side we obtain:

`(A^3)/(A'^3)=(V^2)/(V'^2)`

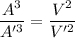
We have:

V=210 m³ , V'=1680 m³

A=856 m²

Hence, we have:

`((856)^3)/(A'^3)=((210)^2)/((1680)^2)\\\\\\A'^3=(107* 2)^3\\\\\\A'=214\ m^2`

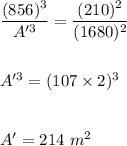
Hence, the surface area of solid is:

214 m²