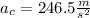Answer:
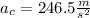
Step-by-step explanation:
The formula for centripetal acceleration is:
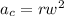
Where,
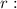 radius.
radius.
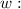 Angular speed.
Angular speed.
Angular speed is defined by:
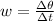
Where,
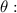 position angle.
position angle.
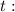 time.
time.
In this case we have that the object takes 4.0 seconds to complete ten revolutions.
You have to know that 1 revolution =
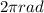 , then
, then
10 revolutions=
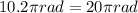
Replacing
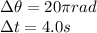
in the formula of Angular speed:
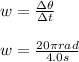
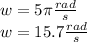
Now we have,
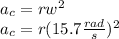
r=1.0m
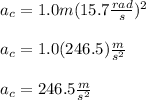
Then the centripetal acceleration is: