Answer:
a = 2
Explanation:
We know that the line of symmetry is equal to -b/2a. Since we know this, we can set up an equation by plugging in certain values.
The line of symmetry equals 2 and the line of symmetry equals -b/2a. By transitivity, 2 equals -b/2a.
In our equation, we are given what b is. b would be the second term in our quadratic equation, which is -8.
Now, we set up our equation and plug in known values.
2 = -b/2a
2 =
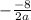
Negatives cancel each other out:
2 =
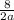
You can solve this part in many different ways, but I will do it using proportions:
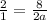
2a *2 = 8 * 1
4a = 8
Divide by 4 on both sides
a = 2
Let me know if you have any questions.