Question

A party rental company has chairs and tables to rent.There were two customers who rented both chairs and tables last week.The table below shows the number of chairs, the number of tables, and the total cost (in dollars) for those two customers.Let x be the cost (in dollars) to rent a chair.Let y be the cost (in dollars) to rent a table.How much does each chair and each table cost (in dollars) to rent?

Answer 1

We can solve this problem with a system of equations.

As stated in the problem x is the cost to rent a chair and y is the cost to rent a table.

So, for the customers, to find our equations, we need to multiply the cost x by the number of chairs (that will give us the cost for the chairs) and we add to that the number of tables multiplied by the cost to rent a table (that will give us the cost for the tables rented) and we equal that sum to the total cost.

So, following that procedure for the first customer we have the equation:

`5x+2y=23`

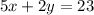
And for the second customer:

`3x+8y=58`

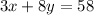
So the system of equations is:

`\begin{gathered} 5x+2y=23 \\ 3x+8y=58 \end{gathered}`

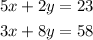
Steps to solve these equations for x and y:

Step 1. Multiply the first equation of the system by -4:

`-4(5x+2y=23)`

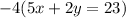
We get the following:

`-20x-8y=-92`

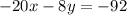
Step 2. to the last equation, add the second equation of our system:

`\begin{gathered} -20x-8y=-92 \\ 3x+8y=58 \\ ----------- \end{gathered}`

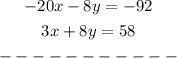
We add the terms with x, and the terms with y, and the independent terms:

`\begin{gathered} -20x-8y=-92 \\ 3x+8y=58 \\ ---------- \\ -17x=-34 \end{gathered}`

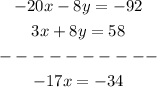
As we can see the terms with y cancel each other.

Step 3. Solve the last equation for x by dividing both sides by -17:

`\begin{gathered} (-17x)/(-17)=(-34)/(-17) \\ x=2 \end{gathered}`

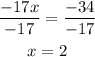
x is equal to 2.

Step 4. Substitute x=2 in the first equation of the system to find the value of y:

`\begin{gathered} \text{First equation of the system:} \\ 5x+2y=23 \\ \text{substituting x=2} \\ 5(2)+2y=23 \\ 10+2y=23 \\ 2y=23-10 \\ 2y=13 \\ y=(13)/(2) \\ y=6.5 \\ \end{gathered}`

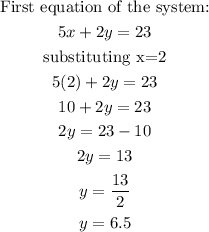
y is equal to 6.5

Answer:

x=2 --> the cost to rent a chair is $2

y=6.5 --> the cost to rent a table is $6.5