Question

Find the surface area of each prism. Round to the nearest tenth if necessary. 8. 15 yd 8 yd 11 yd 17 yd

Answer 1

Here, we are given triangular prism.

To find the surface area of a triangular prism, use the formula below:

`A=2b+h(s1\text{ + s2 + s3)}`

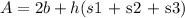
Given:

Side lengths of base, s1 = 17 yd,

s2 = 15 yd

s3 = 8 yd

height, h = 11 yd

b = area of the base

To find the area of the base which is a scalene triangle, use Heron's formula:

`\begin{gathered} A=\sqrt[]{s(s-s1)+(s-s2)+(s-s3)} \\ \\ s=(s1+s2+s3)/(2)=(17+15+8)/(2)=(40)/(2)=20 \\ \\ A=\sqrt[]{20(20-17)(20-15)(20-8)} \\ \\ A=\sqrt[]{20(3)(5)(12)}_{} \\ \\ A=\sqrt[]{3600} \\ \\ A=60\text{ square yards} \end{gathered}`

The area of the base, b = 60 square yards.

To find the surface area of the prism, we have:

`SA=2b+h(s1\text{ + s2 + s3)}`

`\begin{gathered} SA=2(60)+11(17+15+8) \\ \\ SA=120+11(40) \\ \\ SA=120+440 \\ \\ SA=560\text{ square yards} \end{gathered}`

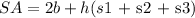
Therefore, the surface area of the triangular prism is 560 square yards

ANSWER:

560 square yards