Question

Barbara buys a box of pens for $4. For every additional box she buys, she gets a $1 discount. Which expression represents the total cost of the pens, c, as a function of the number of boxes, b?

A. c=f(b)=4b-1
B. c=f(b)=4b+1
C. c=f(b)=3b+4
D. c=f(b)=4b+3
E. c=f(b)=4+3(b-1)

Answer 1

E.
`c(b)=4+3(b-1)`

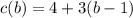
Explanation:

Let b represent the number of boxes.

We have been given that Barbara buys a box of pens for $4, so the cost of 1st box will be $4.

Now the number of boxes without 1st box will be
`b-1`.

We are also told that for every additional box she buys, she gets a $1 discount, so the cost of b boxes without 1st box will be
`3(b-1)`.

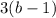The total cost of all the boxes will be cost of 1st box plus cost of b boxes.

`\text{Total cost of boxes}=4+3(b-1)`

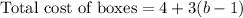
Since we need to represent the total cost of the pens, c, as a function of the number of boxes (b), so our function will be:

`c(b)=4+3(b-1)`

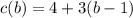
Therefore, our required function is
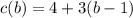`c(b)=4+3(b-1)` and option E is the correct choice.