Question

Bob bought 24 hockey tickets for $83. Adult tickets cost $5.50 and child tickets cost $2.00.How many of each type of ticket did Bob buy?

Answer 1

We have to find how many of each type of ticket did Bob buy.

We can define A as the number of adult tickets and C as the number of child tickets.

The cost for 24 tickets is $83.

Then, we can write for the amount of tickets:

`A+C=24`

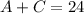
Knowing the price of each type of ticket, we can divide the cost between the cost of the adult tickets and the cost of the child tickets.

The cost for each type will be the number of tickets of each type times the price per ticket of each type.

Then we can write:

`\begin{gathered} 5.50*A+2.00*C=83 \\ 5.5A+2C=83 \end{gathered}`

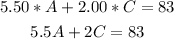
We can express C in function of A using the first equation as:

`\begin{gathered} A+C=24 \\ C=24-A \end{gathered}`

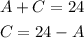
Then we can replace C in the second equation and solve for A as:

`\begin{gathered} 5.5A+2C=83 \\ 5.5A+2(24-A)=83 \\ 5.5A+48-2A=83 \\ 5.5A-2A=83-48 \\ 3.5A=35 \\ A=(35)/(3.5) \\ A=10 \end{gathered}`

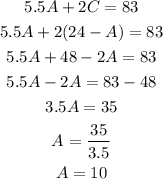
Knowing A = 10, we can calculate C as:

`\begin{gathered} C=24-A \\ C=24-10 \\ C=14 \end{gathered}`

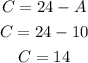
Answer:

Adult tickets: 10

Child tickets: 14