Question

2. The polynomial, p(x) (seen below), is 9th degree. A. Create a table of values that have the x-intercepts of p(x) in the first column and their multiplicities in the second column.B. Write an equation for p(x).

Answer 1

Roots Multiplicity

The multiplicity of a root affects the shape of the graph of a polynomial as follows:

* If the root has odd multiplicity (1, 3, 5, etc), the graph will cross the x-axis at the root.

* If the root has even multiplicity (2,4,6, etc), the graph will touch the x-axis but won't cross it.

As a rule for both cases, when the multiplicity increases, the graph flattens more and more near the root.

With all of the above into consideration, we can see the graph has 3 distinct roots at x=-1, x=1, and x=3 respectively.

The root at x=-1 has an even multiplicity and its shape is steep.

The root at x=1 has an even multiplicity and its shape is more flattened than the other root.

The root at x=2 crosses the x-axis, thus it has odd multiplicity.

A.

Considering the polynomial is of degree 9, the roots and their multiplicities are:

x-intercept multiplicity

-1 2

1 4

2 3

B.

The equation for p(x) is:

`p(x)=a(x+1)^2(x-1)^4(x-2)^3`

The value of a will be determined by the approximate values shown in the graph. For example, for x=0, p(0)=5, thus:

`p(0)=a(0+1)^2(0-1)^4(0-2)^3=a(1)(1)(-8)=5`

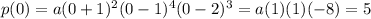
Solving for a, we have a = -5/8

Now the final equation of the polynomial is:

`p(x)=-(5)/(8)(x+1)^2(x-1)^4(x-2)^3`