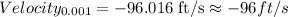Question

estimate the instantaneous velocity at t=7 seconds using the difference quotients with h=0.1,0.01,0.001

Answer 1

EXPLANATION

Given that the arrow function is as follows:

`f(t)=-16t^2+128t`

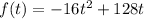
The instantaneous velocity is given by the following relationship:

`(f(t+\Delta t)-f(t))/(\Delta t)\text{ at t=7}`

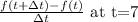
For △t = 0.1:

`Velocity=(\lbrack-16(7+0.1)^2+128\cdot(7+0.1)\rbrack-\lbrack-16\cdot(7)^2+128\cdot7\rbrack)/(0.1)`

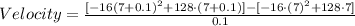
Computing the powers:

`Velocity=(\lbrack-16\cdot50.41+128\cdot7.1\rbrack-\lbrack-16\cdot49+128\cdot7\rbrack)/(0.1)`

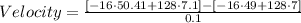
Multiplying numbers:

`Velocity_(0.1)=(\lbrack-806.56+908.8\rbrack-\lbrack-784+896\rbrack)/(0.1)`

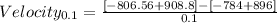
Removing the parentheses and adding numbers:

`Velocity_(0.1)=(-9.76)/(0.1)=-97.6\approx98_{\text{ }}ft/s`

For △t=0.01

`Velocity=(\lbrack-16(7+0.01)^2+128\cdot(7+0.01)\rbrack-\lbrack-16\cdot(7)^2+128\cdot7\rbrack)/(0.01)`

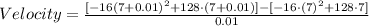
Computing the powers:

`Velocity=(\lbrack-16\cdot49.1401+128\cdot7.01\rbrack-\lbrack-16\cdot49+128\cdot7\rbrack)/(0.01)`

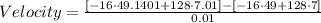
Multiplying numbers:

`Velocity_(0.01)=(\lbrack-786.2416+897.28\rbrack-\lbrack-784+896\rbrack)/(0.01)`

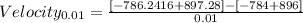
Adding numbers:

`Velocity_(0.01)=(-0.9616)/(0.01)=-96.16\approx-96ft/s`

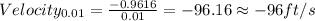
For △t = 0.001

Applying the same reasoning than before, give us the following result:

`Velocity_(0.001)=-96.016\text{ ft/s}\approx-96ft/s`