First, lets see what info we have. The proyectile formula is:
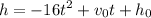
Where v0 is the initial velocity and h0 is the initial speed.
The initial speed is 210ft per second, and since the arrow is shot from ground level, h0 = ft
Thus, the proyectile formula is:
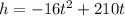
And now we want to find the time the arrow is at 166 ft. This means we want h = 166ft
We write:
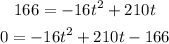
And now we can use the quadratic equation. For a quadratic equation of the form:
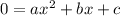
The solutions are:
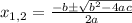
In this case:
a = -16
b = 210
c = -166
We write:
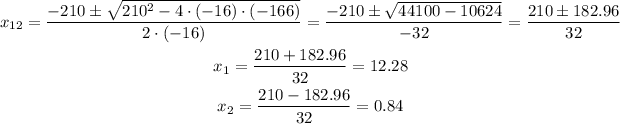
Thus the arrow goes up to 166ft after 0.84 seconds, and then once again (in it's path down) at 12.28 seconds