Question

Peter's farm has 160 meters of fencing, and he wants to fence a rectangular field thatborders a straight river. He needs no fence along the river side. Find the largest areaof Peter's farm that can be fenced.

Answer 1

3200 m²

Step-by-step explanation

Peter wants to build a fence around a rectangular field, except for one side because the river is there,

So, the total perimeter of the fence is,

`P=W+W+L=2W+L`

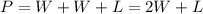
And this is equal to 160 m. Solving for L,

`160=2W+L\text{ }\Rightarrow\text{ }L=160-2W`

The area of this field is,

`A=WL`

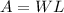
Replace L with the expression we found from the perimeter,

`A=W(160-2W)=160W-2W^2`

The area is given by a quadratic function whose leading coefficient is negative, which means that the graph is a downward parabola and, therefore, the vertex is the maximum value of the area.

The x-coordinate of the vertex is given by,

`f(x)=ax^2+bx+c\text{ }\Rightarrow\text{ }x_(vertex)=(-b)/(2a)`

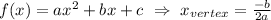
In this case, x is W, a = -2, and b = 160, so the width of the field for the maximum area is,

`W_(vertex)=(-160)/(2(-2))=(160)/(4)=40m`

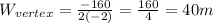
And the length when W = 40 is,

`L=160-2W=160-2\cdot40=160-80=80m`

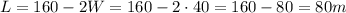
And the area is,

`A=WL=40m\cdot80m=3200m^2`

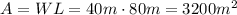
Hence, the largest area of Peter's farm that can be fenced is 3200 square meters.