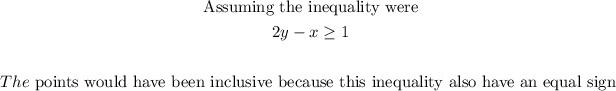The given the initial equation
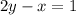
we can determine the part of the graph to be shaded if the equation changes to the inequality:

If we make y the subject of the formula, such that
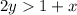
Then we can put in the values of x and y at (0,0)
so that
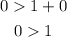
we can see that the expression is false because 0 is not greater than 1
Hence, we will shade away from the origin this means that we will shade above the line
The graph is shown below
So for question B
We will shade above the line
Question C
The points on the line are not included because the inequality does not include an equal sign