Question

Most automobiles have a coolant reservoir to catch radiator fluid that may overflow when the engine is hot. A radiator is made of copper and is filled to its 15.6 L capacity when at 17.5°C. What volume (in L) of radiator fluid will overflow when the radiator and fluid reach their 95.0°C operating temperature, given that the fluid's volume coefficient of expansion is = 400 ✕ 10−6/°C? Note that this coefficient is approximate, because most car radiators have operating temperatures of greater than 95.0°C.

Answer 1

We can use the following formula relating change in volume, change in temperature, and volume coefficient of expansion:

`\Delta V=\beta V_0\Delta T`

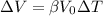
where:

ΔV: change in volume

ΔT: change in temperature

V0: initial volume

Now, the copper radiator also expands when heated along with the fluid, so we need to take that into account. The total change in volume is equal to the sum of the changes in volume of the copper and the fluid.

`\begin{gathered} \Delta V=\Delta V_f+\Delta V_c \\ \Delta V_f:\text{ change in volume of fluid} \\ \Delta V_c:\text{ change in volume of copper} \end{gathered}`

So therefore,

`\Delta V=(\beta_f-\beta_c)V_0\Delta T`

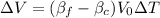
From reference tables and the information given in the problem, we can list the variables we know:

`\begin{gathered} \beta_f=400*10^(-6) \\ \beta_c=51*10^(-6) \\ V_0=15.6 \\ \Delta T=95-17.5=77.5 \end{gathered}`

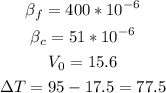
With these variables, we can solve for ΔV.

`\Delta V=(400-51)*10^(-6)*15.6*77.5`

Finally,

ΔV = 0.421941 L