Question

Find the limit as x approaches 3 for the function shown below.g(x) = (x - 3) / (x^2 - 9)

Answer 1

Explanation

We are given the following function:

`g(x)=(x-3)/(x^(^2)-9)`

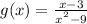
We are required to determine the limit of the function above as it approaches 3.

This is achieved as:

`\begin{gathered} \lim_(x\to3)(x-3)/(x^2-9)=(3-3)/(3^2-9)=(0)/(0) \\ this\text{ }form\text{ }is\text{ }called\text{ }an\text{ }indeterminant\text{ }form \end{gathered}`

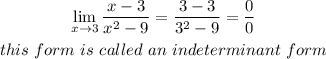
Since the method above cannot give an information on the limit, we need to try another method as follows:

`\begin{gathered} \lim_(x\to3)(x-3)/(x^2-9)=\lim_(x\to3)(x-3)/(x^2-3^2)=\lim_(x\to3)(x-3)/((x-3)(x+3)) \\ =\lim_(x\to3)(1)/(x^+3) \\ =(1)/(3+3)=(1)/(6) \end{gathered}`

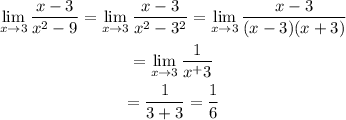
Hence, the answer is 1/6.