Question

Find the equation for the graph of the quadratic function below. Please share all steps and calculations to earn full credit. You may do your work by hand on paper and upload an image of that handwritten work.vertex at (-1,2) and y intercept at y=3

Answer 1

Step 1. The first step is to find the vertex of the parabola, and another point (the y-intercept) located on the parabola.

Those points are:

Where the point is the y-intercept (0,3) and the vertex is at (-1,2)

Step 2. Label the vertex as (h,k)

`\begin{gathered} (h,k)\longrightarrow(-1,2) \\ \downarrow \\ h=-1 \\ k=2 \end{gathered}`

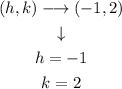
Step 3. Label the point as (x,y):

`\begin{gathered} (x,y)\longrightarrow(0,3) \\ \downarrow \\ x=0 \\ y=3 \end{gathered}`

Step 4. Use the vertex form of the quadratic equation:

`y=a(x-h)^2+k`

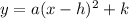
Where h and k are related to the vertex of the parabola.

From this equation, we need to find the value of a.

We find the value of a by substituting the values from step 3 and step 2:

`\begin{gathered} y=a(x-h)^2+k \\ \downarrow \\ 3=a(0-(-1))^2+2 \end{gathered}`

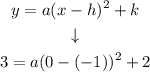
Solving for a:

`\begin{gathered} 3=a(1)^2+2 \\ \downarrow \\ 3=a+2 \\ 3-2=a \\ 1=a \end{gathered}`

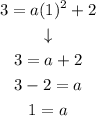
The value of a is 1.

Step 5. The final step is to go back to the vertex form of the quadratic equation:

`y=a(x-h)^2+k`

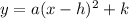
and substitute the known values for a, h and k:

`y=1(x-(-1))^2+2`

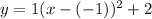
Simplifying:

`y=(x+1)^2+2`

This is the equation of the graph.

Answer:

`y=(x+1)^2+2`