Question

A signal flare is fired into the air from a boat. The height h of the flare in feet after t seconds is h = -16t2 + 160t. How high will the flare travel? When will it reach this maximum height? When will the flare hit the water? After 8 seconds is the flare going up on coming down? How high is it at that time? Approximately how many seconds is the flare above 250 feet? Summary of what’s happening in the problem

Answer 1

The equation that models the height of the flare is a quadratic equation, then the maximum height corresponds to the vertex.

The vertex of a quadratic equation is found as follows:

`t_V=(-b)/(2\cdot a)`

where a and b are the first two coefficients of the quadratic equation, and tv is the time at which the maximum height is reached. In this case, a = -16, and b = 160, therefore:

`\begin{gathered} t_V=(-160)/(2\cdot(-16)) \\ t_V=(-160)/(-32) \\ t_V=5\text{ seconds} \end{gathered}`

To find the height we need to replace this time t into the equation as follows:

`\begin{gathered} h_V=-16t^2_V+160t_V \\ h_V=-16\cdot5^2+160\cdot5 \\ h_V=-400+800 \\ h_V=400\text{ ft} \end{gathered}`

How high will the flare travel? 400 ft.

When will it reach this maximum height? After 5 seconds.

If the flare hits the water, the heigh is of the flare is zero, then:

`\begin{gathered} h=-16t^2+160t \\ \text{ Taking 16t as common factor} \\ 0=16t(-t+10) \\ \text{ This equation has two solutions:} \\ 16t=0 \\ t_1=0 \\ Or \\ -t+10=0 \\ 10=t_2 \end{gathered}`

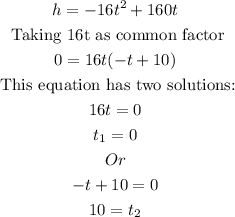
When will the flare hit the water? After 10 seconds

After 8 seconds is the flare going up on coming down? Going down. 8 seconds comes after the maximum height and before the flare reaches the water.

To find the height at time = 8 seconds, we need to replace this time t into the equation as follows:

`\begin{gathered} h=-16\cdot8^2+160\cdot8 \\ h=-1024+1280 \\ h=256\text{ ft} \end{gathered}`

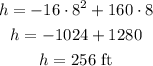
How high is it at that time? It is at 256 ft high.

To find the time elapsed when the height, h, is 250 ft, we need to replace this value into the quadratic equation and solve for time, t.

`\begin{gathered} 250=-16t^2+160t \\ 0=-16t^2+160t-250 \end{gathered}`

Using the quadratic formula:

`\begin{gathered} t_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ t_(1,2)=\frac{-160\pm\sqrt[]{160^2-4\cdot(-16)\cdot(-250)}}{2\cdot(-16)} \\ t_(1,2)=\frac{-160\pm\sqrt[]{9600}}{-32} \\ t_1\approx(-160+98)/(-32)\approx1.9\text{ seconds} \\ t_2\approx(-160-98)/(-32)\approx8\text{ seconds} \end{gathered}`

The flare reaches this heigth after approximately 1.9 seconds, after this, it is above this height until 8 seconds elapsed from the beginning.

Approximately how many seconds is the flare above 250 feet? 6.1 seconds (= 8 - 1.9).

Summary of what’s happening in the problem. At the beginning the flare is at the level of the water (at t = 0, h = 0). Then its height, h, starts to increase until it reaches its maximum of 400 ft high, after 5 seconds (when t = 5, h = 400). Next, the flare starts to fall down until it reaches the water, this happen after 10 seconds (at t = 10, h = 0).