First, draw a diagram to visualize the situation:
The directions of the forces are shown in the diagram. Remember that charges with opposite sign attract each other, while charges with the same sign repel each other.
Use Coulomb's Law to find the magnitude of each force. Next, find the X and Y components of each force. Next, combine the components to find the components of the net force, and finally, use the components of the net force to find the magnitude of the force on a 1μC charge placed at the center of the square.
The distance between the center of a square with length L and its corner is:
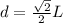
Then, the distance between the charge at the center of the square and the rest of the charges is:
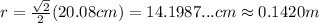
According to Coulomb's Law, the force between two charged particles separated by a distance r is:
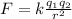
Where k is the Coulomb's Constant:
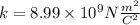
Calculate the magnitude of the force that each charge on the corner of the square creates over the charge at the center:
+12.21μC:
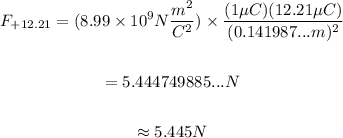
-16.95μC:
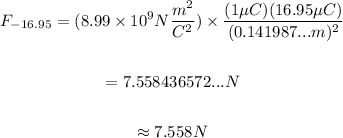
-7.62μC:
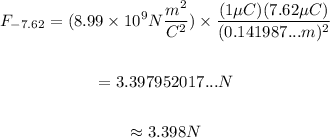
+13.6μC:
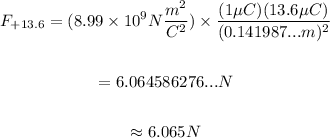
Notice that two pairs of forces act in the same direction, so we can add them arithmetically:
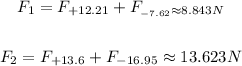
These forces act on the particle at the center according to the following diagram:
As we can see from the diagram, the forces of 8.8N and 13.6N are perpendicular, so the net force turns out to be the diagonal of a rectangle whose sides measure F1 and F2.
Then, instead of finding the vertical and horizontal components of each force, we can see from the Pythagorean Theorem that the magnitude of the net force is given by:

Therefore, the magnitude of the force on a 1microCoulomb charge placed at the center of the square, is approximately 16.24N.