Question

1. Which one of the following is a polynomial function? (1.f(x) = -4*+21S(x)= 3x-2x + x f(x)=-5x* = 32f(x)= x + V3x-7

Answer 1

To answer this question, we need to take into account that:

1. A polynomial is a finite sum of terms.

2. All the variables have a whole number as an exponent.

3. None of the variables appear in a denominator.

Having this information, we can say that:

First case:

`f(x)=-4^(2x)+2x^2`

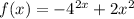
We can see that this IS NOT a polynomial, in the sense that the term -4^(2x) is an exponential function.

Second Case:

`f(x|)=3x^3-2x^(-2)+x=3x^3-(2)/(x^2)+x`

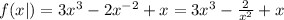
For this case, we see that in the second term, the variable appears in the denominator. Therefore, this is NOT a polynomial function.

Third Case:

`f(x)=-5x^(-2)-3x^(-2)=-(5)/(x^2)-(3)/(x^2)`

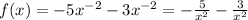
This case is similar to the previous one. Then, this is NOT a polynomial function.

Fourth Case:

`f(x)=x^2+\sqrt[]{3}x-7`

In this case, we can see that the exponents in the variables are whole numbers (2 and 1). None of the variables appear in the denominator, and it is a finite number of terms. Therefore, this IS a polynomial function (even if it has radical 3).

Hence, the only function that is a polynomial is option D.