Question

The product of two positive numbers is 750. The first number is 5 less than the second number. The equation x(x – 5) = 750 can be used to find x, the value of the greater number.

What is the value of the greater number?

a. 15
b. 25
c. 30
d. 50

Answer 1

ab=750 and a=b-5, using this value of a in the original equation gives you:

(b-5)b=750

b^2-5b=750

b^2-5b-750=0

b^2-30b+25b-750=0

b(b-30)+25(b-30)=0

(b+25)(b-30)=0

b=30

Answer 2

c. 30

Explanation:

Here x represents the greater number or second number,

Since, The smaller number is 5 less than the greater number,

Thus, the smaller number = (x - 5)

Given,

The product of x and (x-5) is 750

⇒ x(x-5) = 750

`x^2-5x=750` ( By associative property )

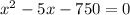`x^2-5x-750=0` ( By subtracting 750 on both sides )

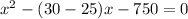`x^2-(30-25)x-750=0` ( By middle term splitting )

`x^2-30x+25x-750=0`

`x(x-30)+25(x-30)=0`

`(x-30)(x+25)=0`

`\implies x = 30\text{ or } x = -25`

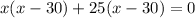
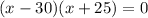
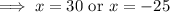
But, both numbers are positive

⇒ x can not be negative in the given question.

Hence, the value of greater number is 30.

Option C is correct.