Question

Suppose the altitude to the hypotenuse of a right triangle bisects the hypotenuse. How does the length of the altitude compare with the lengths of the segments of the hypotenuse?

a) The length of the altitude is equal to twice the length of one of the segments of the hypotenuse.
b) The length of the altitude is equal to half the length of one of the segments of the hypotenuse.
c) The length of the altitude is equal to the length of one of the segments of the hypotenuse.
d) The length of the altitude is equal to the sum of the lengths of the segments of the hypotenuse.

Answer 1

1. On a right triangle, how does the length of the median drawn to the ... lengths. D. C. B. A. Triangle ABC is a right triangle with is the median to the ... to the hypotenuse is one-half as long as the hypotenuse, ..... This segment is an altitude to both triangles, with bases. AD and DC. These two segments are equal in length.

Answer 2

Option: C is correct.

c) The length of the altitude is equal to the length of one of the segments of the hypotenuse.

Explanation:

By the Right Triangle Altitude Theorem:

The measure of the altitude drawn from the vertex of the right angle of a right triangle to its hypotenuse is the geometric mean between the measures of the two segments of the hypotenuse.

From the figure we could say that:

`AD=√(CD\cdot DB)`

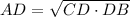
As the hypotenuse is divided into divided into two equal parts since the altitude bisects the hypotenuse of the right triangle.

This means that:

CD=DB

Hence,

`AD=\sqrt{CD^(2)}\\\\AD=CD`

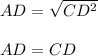
Hence, we could say that:

c) The length of the altitude is equal to the length of one of the segments of the hypotenuse.