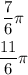Remember the following trigonometric identities:
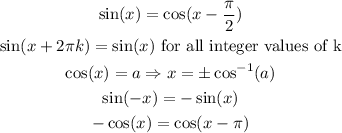
Using these identities, search for an angle x such that:
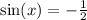
Write the sine of x in terms of the cosine:
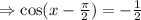
Multiply both sides by -1:
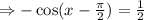
Since -cos(x)=cos(x-π), then:
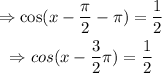
Use the inverse cosine function to isolate x-3π/2:
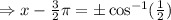
Since cos(π/3) = 1/2, then cos^-1(1/2) = π/3:
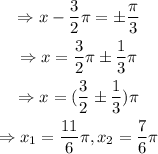
To find other values of x which make sin(x) equal to -1/2, we can add integer multiples of 2π to the values x₁ and x₂. In this case, since all options are less than 2π, that is not necessary.
Therefore, the angles whose sine is -1/2 are: