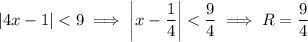You can use the root test here. The series will converge if
![L=\displaystyle\lim_(n\to\infty)\sqrt[n]{((4-x)^n)/(4^n+9^n)}<1](https://img.qammunity.org/2018/formulas/mathematics/college/d8dwfhv99dy9sr92kh7xwfz2psp2gcnk1c.png)
You have
![L=\displaystyle\lim_(n\to\infty)\sqrt[n]{((4-x)^n)/(4^n+9^n)}=|4-x|\lim_(n\to\infty)\frac1{\sqrt[n]{4^n+9^n}}](https://img.qammunity.org/2018/formulas/mathematics/college/gi3a06ksttcdkost3xge81m427lldauz8j.png)
Notice that
![\frac1{\sqrt[n]{4^n+9^n}}=\frac1{\sqrt[n]{9^n}\sqrt[n]{1+\left(\frac49\right)^n}}=\frac1{9\sqrt[n]{1+\left(\frac49\right)^n}}](https://img.qammunity.org/2018/formulas/mathematics/college/hzupze50d78t3vxfw3fhcelw3ktfjjyrmh.png)
so as
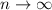
, you have
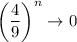
, which means you end up with
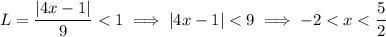
This is the interval of convergence. The radius of convergence can be determined by finding the half-length of the interval, or by solving the inequality in terms of
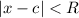
so that
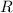
is the ROC. You get