Answer: 85
To solve this, we need to calculate the height of the triangle. To do this, we divide the triangle verticaly, in two right triangles.
So, we have the hypotenuse of the two smaller triangles is 14. The short leg is half the side of the big triangle: 14/2=7 and the long leg is the height of the triangle and what we want to know.
By the pythagorean theorem:
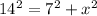
![x=\sqrt[]{14^2-7^2}=7\sqrt[]{3}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/apzlrofmq23ms5d8q3y0.png)
And now we use the formula for the area of a triangle:
![A=(b\cdot h)/(2)=\frac{7\cdot7\sqrt[]{3}}{2}=\frac{49\sqrt[]{3}}{2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ktujywq1w6kjajsuxphu.png)
This is the area of each of the smaller triangles. To get the area of the big triangle, we add up the two smaller areas:
![\frac{49\sqrt[]{3}}{2}+\frac{49\sqrt[]{3}}{2}=49\sqrt[]{3}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/p2lz58a5kpakwlddeorx.png)
rounded to the nearest tenth is 85