Question

Number 6. Find the missing measure and round to nearest 10th

Answer 1

Note that Cosine law can be used if three sides of the triangle are given in order to get the angles.

For example, in getting the measurement of angle C

`\cos C=(a^2+b^2-c^2)/(2ab)`

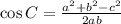
Then take the arccos to get the angle C.

From the problem, we have :

We need to find the measurement of angle F using the same formula above.

`\begin{gathered} \cos F=(16^2+12^2-18^2)/(2(16)(12)) \\ \cos F=(19)/(96) \end{gathered}`

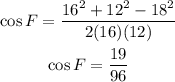
Taking the arc cosine :

`\begin{gathered} \angle F=\arccos ((19)/(96)) \\ \angle F=78.58 \end{gathered}`

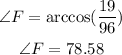
The answer rounded to the nearest 10th is