The given graph gives a linear relationship between the driving time 'x' and the remaining distance 'y'.
Since the relationship is linear with slope -0.85, its equation is given by,
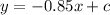
Here 'c' is the y-intercept.
At x=38, the value is y=49,
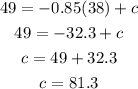
Substitute the value in the equation,

Now, solve for 'y' when the value of 'x' is 22,
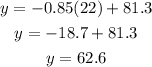
Thus, 62.6 miles were remaining after 22 minutes of driving.