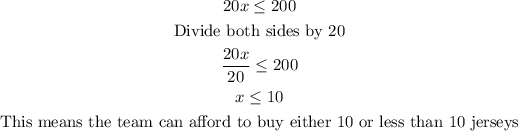Question

can you answer all of theseTranslate story problems into equations ? Solve equations?Translate story problems into inequalities? Graph inequalities on the number lines?Identify inverse operations?Identify and explain independent & dependent variables? Analyze relationships between two variables from a graph?Represent a relationship between two variables as an equation, table or graph?

Answer 1

(1) To solve equations basically means to find the unknown value when two expressions equal each other. You have an equation when one expression is written as "equal to" another one. For example,

10 = 10 (is an equation)

x = 5 (is an equation)

2x + 5 = 15 (is an equation)

Where the sign "equal to" is not inserted, then you do not have an equation

In the third example above, we can solve the equation by removing the known value in the expression and then we are left with the unknown value. The known value is x, therefore we remove positive 5. To do that, subtract 5 from 2x + 5. It is extrememly important to note that whatever we do to the left side, we must also do to the right side. That means we also subtract 5 from the right side. Hence;

2x + 5 - 5 = 15 - 5

2x+ 0 = 10

2x = 10

We still have 2 to remove and to do that, we divide both sides by 2

`\begin{gathered} (2x)/(2)=(10)/(2) \\ x=5 \end{gathered}`

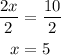
Note that when the known value is a positive one, then e subtract, and when it is a negative one we add. Also when two expressions are written together, to remove one of them, we would have to divide by the other one. Eg, when you have 3y, and you need y to stand alone, you divide by 3 (like we did with 2x in the example above).

The question requires you to translate a word problem into an equation. Therefore, we would take a random illustration to explain this.

Lanayah earns a certain amount as weekly earnings. Twice her earnings plus 20 would be equal to Frazer's weekly earnings. If Frazer earns $120 weekly, how much is Lanayah's earnings?

Solution:

Let Lanayah's earnings be represented by x. Twice her earnings means 2 times x, or better still, 2x. This plus 20 would mean 2x + 20, and this is equal to Frazer's weekly earnings. If Frazer earns $120 weekly, then the word problem becomes;

`2x+20=120`

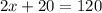
(2) To solve the equation (like explained above);

`\begin{gathered} 2x+20=120 \\ \text{Subtract 20 from both sides} \\ 2x+20-20=120-20 \\ 2x=100 \\ \text{Divide both sides by 2} \\ (2x)/(2)=(100)/(2) \\ x=50 \\ \text{Therefore, Lanayah earns \$50 weekly} \end{gathered}`

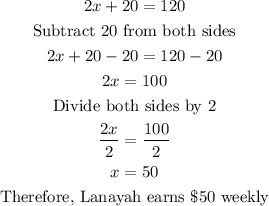
(3) To translate word problems into inequalities, example;

The school soccer team needs to buy jerseys for its 20 members and has a budget of $200. Soccer jerseys cost a certain amount per unit. Write an inequality to show how many jerseys the team can possibly afford.

Solution:

Let the amount of each jersey be represented by x. That means x multiplied by 20 (number of teammates) would result in the total amount to be spent. However, the team has a budget of 200 which means they cannot exceed that amount. Therefore,

20 times x, or better still, 20x would be equal to 200. But since we do not know the amount per unit and we cannot spend above $200, we can now express this as,

`20x\leq200`

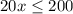
The solution therefore is;

`\begin{gathered} 20x\leq200 \\ \text{Divide both sides by 20} \\ (20x)/(20)\leq200 \\ x\leq10 \\ \text{This means the team can afford to buy either 10 or less than 10 jerseys} \end{gathered}`