Question

Suppose that the number of bacteria in a certain population increases according to a continuous exponential growth model. A sample of 2300 bacteriaselected from this population reached the size of 2450 bacteria in two hours. Find the hourly growth rate parameter.Note: This is a continuous exponential growth model.Write your answer as a percentage. Do not round any intermediate computations, and round your percentage to the nearest hundredth.

Answer 1

The general exponential growth model is defined as

`y(t)=y_0e^(kt)`

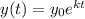
Here ley y be the population of a bacteria at ttime in hours, k is the growth parameter, t is the time, y0 is the initial population of the bacteria.

Accoridng to this problem the initial population is 2300.

So,

`y_0=2300.`
`y(t)=2300e^(kt)`

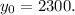
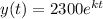
It is given that after 2 hours, the population of the bacetria is 2450.

That is, at time t=2,y=2450.

`\begin{gathered} y(t)=2300e^(kt) \\ y(2)=2300e^(k\cdot2) \\ 2450=2300e^(2k) \\ (2450)/(2300)=e^(2k) \\ (49)/(46)=e^(2k) \\ \ln ((49)/(46))=\ln (e^(2k)) \\ \ln ((49)/(46))=2k \\ (1)/(2)\ln ((49)/(46))=k \\ 0.031582=k \end{gathered}`

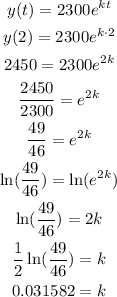
Now to get the percentage multiply the obatined k value by 100.

`\begin{gathered} k=0.031582\cdot100 \\ =3.1582 \\ =3.16 \end{gathered}`

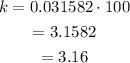
So, the required growth rate is k=3.16%.