Question

farmer ed has 900 meters of fencing and wants to enclose a rectangular plot that borders on the river. if farmer ed does not fence the side along the river . find the length and the width of the plot that will maximize the area. what is the largest area that can be enclosed.

Answer 1

the largest area can be enclosed by 300 meters per side along the fence
hoped this helped

Answer 2

Maximum area enclosed will be 101250 meter².

Explanation:

Let the length of the rectangular plot is x meters and the width is y meters.

900 meters is the length of the fence which represents the length of the three sides of the plot.

Therefore,

x + 2y = 900

y =
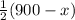`(1)/(2)(900-x)` meters

Now the area of the rectangular plot will be

A = Length × Width

= (x)(y)

=
`(1)/(2)x(900-x)`

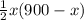
= 450x -
`(x^(2))/(2)`

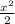
We know for the maximum area we will differentiate the area and equalize it t the zero.

`(dA)/(dx)=(d)/(dx)(450x-(x^(2))/(2))`

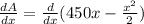
= 450 - x

For the maximum area,
`(dA)/(dx)=0`

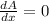
Therefore, 450 - x = 0

x = 450

and y =
`(1)/(2)(900-x)`

y =
`(1)/(2)(900-450)`

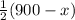
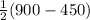
y = 450 - 225

= 225 meters

Now the area enclosed A = 450 × 225

A = 101250 meter²