Question

-8x+6y=12 8x+10y=20 elimination

Answer 1

The given system of equation is:

`\begin{gathered} -8x+6y=12\text{ Equation 1} \\ 8x+10y=20\text{ Equation 2} \end{gathered}`

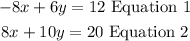
First, add the second equation to the first one:

`\begin{gathered} -8x+6y=12 \\ +8y+10y=20 \\ ----------- \\ 0x+16y=32 \end{gathered}`

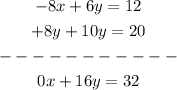
Now, we obtain this new equation:

`16y=32`

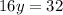
Now, divide both sides by 16:

`\begin{gathered} (16y)/(16)=(32)/(16) \\ \text{Simplify} \\ y=2 \end{gathered}`

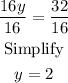
Now, substitute the y-value into equation 1 and solve for x:

`\begin{gathered} -8x+6(2)=12 \\ -8x+12=12 \\ \text{Subtract 12 from both sides} \\ -8x+12-12=12-12 \\ -8x=0 \\ \text{Divide both sides by -8} \\ (-8x)/(-8)=(0)/(-8) \\ \text{Simplify} \\ x=0 \end{gathered}`

Then, the solution to the system is x=0 and y=2.