Question

Two angles are supplementary (sum of180°). One angle is 3° less than twice theother. What are the measurements of thetwo angles?

Answer 1

We know that the angles add up to 180° and we also know that one angle is 3° less than twice the other.

Now, we can represent the situation using a system of equations

`\begin{cases}x+y=180^(\circ)\ldots(1) \\ 2y-3^(\circ)=x\ldots(2)\end{cases}`

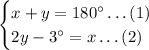
Where,

- x represents the measure of one angle

- y represents the measure of the second angle

Then, we must solve the sysyem of equations

1. we can multiply the first equation by -2

`\begin{gathered} -2(x+y)=-2(180^(\circ)) \\ -2x-2y=-360^(\circ)\ldots(3) \end{gathered}`

2. we can rewrite the equation (2) as

`-x+2y=3^(\circ)`

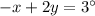
3. We must add up equations (2) and (3)

`\begin{gathered} -x+2y=3^(\circ) \\ -2x-2y=-360^(\circ) \\ ------------- \\ -3x=-357^(\circ)\ldots(4) \end{gathered}`

4. We can solve equation (4) for x

`\begin{gathered} -3x=-357^(\circ) \\ x=(-357^(\circ))/(-3) \\ x=119^(\circ) \end{gathered}`

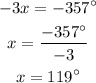
5. We must replace x = 119° in equation (1) and then we must solve for y

`\begin{gathered} 119^(\circ)+y=180^(\circ) \\ y=180^(\circ)-119^(\circ) \\ y=61^(\circ) \end{gathered}`

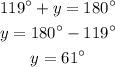
Finally, the measurements of the two angles are 119° and 61°