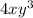Answer:
Greatest common factor(GCF) of a polynomial states that the largest polynomial that divides into the polynomials.
Given that:
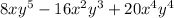
First find the GCF of the expression.
The GCF of 8, 16 and 20 is 4.
The GCF of
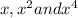 is x.
is x.
And the
GCF of
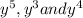 is
is
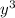
Combine these to find the GCF of the polynomial is,
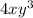
then;
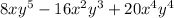 =
=
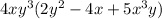
Therefore, the greatest common factor of
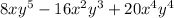 is
is