Question

A. How many zeros does the function have over the set of complex numbers?B. What is the maximum number of local extrema (maxima or minima) the graph of the function can have?C. What value does the function (y) approach as x approaches infinity and negative infinityD. List the possible rational zeros of this functionE. Factor this polynomial completely over the set of complex numbers.

Answer 1

Given the function:

`f(x)=x^3-x^2-4x+4`

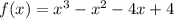
A. How many zeros does the function have over the set of complex numbers?

The function has 3 zeros because the degree of the function is the third degree.

B. What is the maximum number of local extrema (maxima or minima) the graph of the function can have?

To answer the question, we will graph the function.

The graph of the function is as shown in the following picture:

As shown, the function has a local maximum at ( -0.87, 6.06 )

And a local minimum at ( 1.54, -0.88 )

So, the function has 2 points of local extrema.

D. List the possible rational zeros of this function.

The zeros of the function are the values of x which make the function = 0

the zeros are also, is the intersection between the function and the x-axis.

as shown in the figure, the function has 3 zeros at x = { -2, 1, 2 }

E. Factor this polynomial completely over the set of complex numbers.

`\begin{gathered} f(x)=x^3-x^2-4x+4 \\ f(x)=x^2(x-1)-4(x-1) \\ f(x)=(x^2-4)(x-1) \\ f(x)=(x+2)(x-2)(x-1) \end{gathered}`

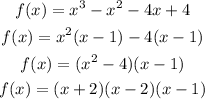
So, the factor of the functio is: f(x) = (x+2)(x-2)(x-1)