Question

Integrate f(x,y,z)=x over the region in the first octant (x>0, y>0, z>0) above z=y^2 and below z=8-2x^2-y^2

Answer 1

`\begin{cases}z=y^2\\z=8-2x^2-y^2\end{cases}\implies y^2=8-2x^2-y^2\iff y^2+x^2=4`

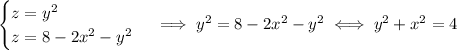
which means the intersection of the parabolic cylinder
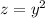
`z=y^2` and paraboloid
`z=8-2x^2-y^2` is a circle of radius 2 centered at the origin.

So the integral can be represented in Cartesian coordinates by


`\displaystyle\iiint_D x\,\mathrm dV=\int_(-2)^2\int_(-√(4-x^2))^(√(4-x^2))\int_(y^2)^(8-2x^2-y^2)x\,\mathrm dz\,\mathrm dy\,\mathrm dx`

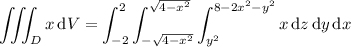
where
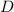
`D` is the region between the two surfaces.

Converting to cylindrical coordinates will make this slightly easier to compute.


`\begin{cases}x(r,\theta,\zeta)=r\cos\theta\\y(r,\theta,\zeta)=r\sin\theta\\z(r,\theta,\zeta)=\zeta\end{cases}`

`\implies(\partial(x,y,z))/(\partial(r,\theta,\zeta))=\begin{vmatrix}x_r&x_\theta&x_\zeta\\y_r&y_\theta&y_\zeta\\z_r&z_\theta&z_\zeta\end{vmatrix}=\begin{vmatrix}\cos\theta&-r\sin\theta&0\\\sin t&r\cos t&0\\0&0&1\end{vmatrix}=r`

Letting
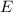
`E` denote the same region in cylindrical coordinates, you have


`\displaystyle\iiint_E r\cos\theta\left|(\partial(x,y,z))/(\partial(r,\theta,\zeta))\right|\,\mathrm dV=\int_0^(2\pi)\int_0^2\int_(r^2\sin^2\theta)^(8-r^2(1+\cos^2\theta))r^2\cos\theta\,\mathrm d\zeta\,\mathrm dr\,\mathrm d\theta`

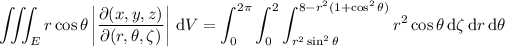
In either case the integral reduces to 0.