Question

When 2x^2/y = w+2/4 is solved for w, one equation is

Answer 1

B, because you can cancel the y in -2y and the answer will still be the same

Hope this helps :)

Answer 2

Answer: w=
`(8x^(2) - 2y )/(y)`

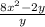
Explanation:

From the question above, we have;

`(2x^(2) )/(y) = (w + 2)/(4)`

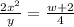
We will have to make w subject of the formula. To do that we will first have to cross multiply

2x² × 4 = (w +2) y

8x² = (w + 2 ) y

we will now divide both-side of the equation by y

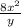`(8x^(2) )/(y)` = w + 2

we will then subtract 2 from both-side of the equation

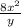`(8x^(2) )/(y)` - 2 = w

We shall now make the left hand side of the equation a standard fraction

`(8x^(2) - 2y)/(y)` = w

Therefore w =
`(8x^(2) - 2y)/(y)`