Given:
The equation is:
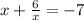
Find-:
Restrictions for this equation
Step-by-step explanation:
The equation is:
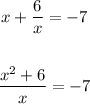
The denominator is not equal to zero. If the denominator is zero, then the function is undefined.
Then the restriction is:
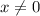
For the function value of x is:
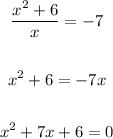
The value of "x" is:
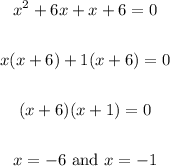
So above function value of x is possible only -6 and -1 then the restriction value is all real numbers except only -6 and -1
