We know that
• The mass is m = 30.0 kg.
,
• The vertical height is h = 10.0 m.
(a)
We have to use the conservation of energy theorem, which states that mechanical energy is constant all the time. Also, halfway down means a height of 5.0 m. It's important to know that at the top the total energy is potential, while halfway is distributed as kinetic and potential, the expression below shows this

Then, using the definition of each energy, we have
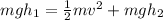
Now, we use the given values to find the speed.
![\begin{gathered} \text{mgh}_1=m((1)/(2)v^2+gh_2) \\ gh_1=(1)/(2)v^2+gh_2 \\ 9.81m/s^2\cdot10m=(1)/(2)v^2+9.81m/s^2\cdot5m \\ 98.1m^2/s^2=(1)/(2)v^2+49.05m^2/s^2 \\ 98.1m^2/s^2-49.05m^2/s^2=(1)/(2)v^2 \\ 2\cdot49.05m^2/s^2=v^2 \\ v=\sqrt[]{98.1m^2/s^2} \\ v\approx9.9m/s \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/m5l73r6w43g7b2w6122p.png)
Therefore, the speed of the child halfway down is 9.9 meters per second.
(b)
In this case, we just have to use as the second height of the equation the magnitude 2.5 meters because that's 3/4 of the way down. So, let's use the same process and expression
![\begin{gathered} gh_1=(1)/(2)v^2+gh_2 \\ 9.81m/s^2\cdot10m=(1)/(2)v^2+9.81m/s^2\cdot2.5m \\ v=\sqrt[]{2(98.1m^2/s^2-24.53m^2/s^2)} \\ v\approx12.1m/s \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/gna90y6nfnhjy044e7xu.png)
Therefore, the speed of the child 3/4 of the way down is 12.1 meters per second.