Question

For the function f(x) = x2 + 3, find the slope of the tangent line at x = 11.

Answer 1

Given:

The function is

`f(x)=x^2+3`

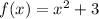
To find:

The slope of the tangent line at x = 11.

Solution:

The slope of the tangent is the value of f'(x) at x=11.

We have,

`f(x)=x^2+3`

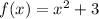
Differentiate with respect to x.

`f'(x)=2x+0`
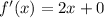
`\left[\because (d)/(dx)x^n=nx^(n-1),(d)/(dx)C=0,\text{ where C is constant}\right]`

`f'(x)=2x`

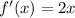
Substitute x=11 in the above equation.

`f'(11)=2(11)`

`f'(11)=22`

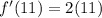
Therefore, the slope of the tangent at x=11 is 22.